Chapter 1: The Fibonacci Sequence and Its Origins

The Fibonacci sequence is a fascinating mathematical construct where each number is derived by adding the two preceding numbers, beginning with 0 and 1:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…

Although named after the Italian mathematician Fibonacci, who popularized it in his 1202 work "Liber Abaci," its origins trace back to the ancient Indian mathematician Acharya Pingala, who explored this sequence around 200 BCE in relation to poetic meter. Thus, while Fibonacci introduced this sequence to the Western world, it is essential to acknowledge its earlier roots in Eastern mathematics.

A particular ratio emerges from the Fibonacci sequence, leading to what is termed the Golden Ratio:

1:1.618

This ratio can be visualized by dividing a line segment into two parts, denoted as “a” and “b,” such that the ratio of a to b mirrors the ratio of the entire segment (a + b) to the larger segment (a). This can be expressed mathematically as:

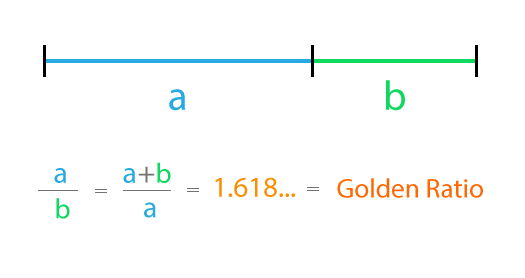
The Golden Ratio represents a profound mathematical entity, often deemed the most irrational of all irrational numbers. An irrational number cannot be expressed as a fraction of two integers. Although the Golden Ratio is an irrational number that continues indefinitely, it simplifies to a growth rate of 1 to 1.618. This ratio is symbolized by phi (φ) and is illustrated by the Golden Rectangle, where the longer side is 1.618 times the shorter side. A rectangle with this aspect ratio can be infinitely subdivided into a square and a Golden Rectangle, leading to the formation of a Golden Spiral with a growth factor of φ:

Furthermore, the Golden Ratio can be expressed in relation to its reciprocal:

φ = (1/φ + 1)

This relationship can be formulated into the quadratic equation:

φ² - φ - 1 = 0

The equation yields two conjugate solutions, one positive and one negative:

(1 + √5)/2

(1 - √5)/2

However, since φ represents a ratio of lengths, only the positive solution is relevant. The negative reciprocal corresponds to the conjugate of φ. Understanding the distinction between infinite irrational numbers and finite rational numbers is crucial. For example, the fraction 23/16 corresponds to 1 plus 1 over 2 plus 1 over 3 plus 1 over 2—a finite continued fraction. This contrasts with the boundless elegance of φ. Notably, the first denominator in this fraction mirrors the entire continued fraction:

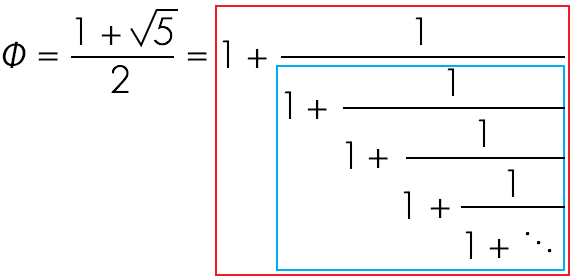
By truncating the continued fraction after each nesting level, we observe:

1/1, 2/1, 3/2, 5/3,…

These fractions provide the best rational approximations to φ with a denominator of that value or lower, precisely mirroring the ratios of successive Fibonacci numbers. More significantly, as the limit extends toward infinity, these approximations converge on φ.

Chapter 2: The Golden Ratio in Nature and Design

The Golden Ratio is not merely a mathematical curiosity; it permeates various fields and is utilized for calculations, applications, and inspiration. Its presence is ubiquitous in nature, manifesting in a myriad of forms, both living and non-living. In design, the Golden Ratio often leads to organic compositions that are aesthetically pleasing. This natural inclination towards the divine curve of the Golden Spiral resonates with a profound sense of spiritual geometry within us. Our perception is inherently tuned to appreciate shapes that embody the Golden Ratio, a fact that has influenced great artists, from Leonardo da Vinci to Salvador Dali, in crafting visually harmonious masterpieces.

Ultimately, the Golden Ratio holds a unique significance that transcends mere numbers. It embodies a purposeful essence within mathematics and beyond:

1.61803398874989484820458…