# Exploring Quantum Computational Complexity in Black Holes
Written on
Chapter 1: Understanding Quantum Complexity
In this exploration, we discuss how straightforward rules, such as Efimov effects, can give rise to intricate phenomena within the realm of quantum computational complexity, particularly concerning black holes. This piece builds on previous discussions regarding the origins of force fields and aims to illuminate how mathematics may have played a pivotal role in the formation of our universe.
Describing the constituents of AdS force fields as "particles" can be somewhat misleading, as this term simplifies the complex mathematical nature of the content within these fields. Nevertheless, using the term "particle" helps convey the idea of how these entities can evolve and become more intricate over time. Particles undergo cycles between black and white holes, and through Efimov effects, their complexity is enhanced.
A particle located at the boundary of an AdS black hole can be conceptualized as a hologram—a mathematical representation existing in one less dimension. The emergence of new characteristics due to the Efimov effect in the AdS boundary leads to increasingly intricate holographic representations. For instance, in a four-dimensional AdS space, black holes might possess five internal dimensions (including two time-like dimensions), resulting in boundaries that showcase four-dimensional holographic projections. These projections could arise from white holes within the original four-dimensional AdS space.
When these four-dimensional holographic entities integrate into the foundational AdS space, the characteristics of that space change, even if the content remains static. The new entities carry information generated by Efimov effects within black holes, altering the mathematical description of AdS space to include features absent in the original three-dimensional configuration.
As particles are absorbed into black holes, the content contained within does not need to "recreate" the quantum phenomena, force fields, and mass each time. The outcomes of countless iterations are already encoded within the mathematical frameworks of the particles entering black holes. Notably, the constraints of our universe's duration need not limit the permutations available for the development of complex life on Earth; countless prior iterations of our universe might have existed before the one we currently inhabit.
Chapter 2: Entropy and Efimov Effects
The interplay between Efimov effects and Noether symmetry illustrates how complex mathematical forms can arise naturally within AdS space. A black hole in this context maintains a finite size, continuously growing until it ultimately collapses. The finite nature of the black hole's content implies there are limited ways to arrange this information. Information entropy serves as a mathematical tool to analyze the distribution of information within a space, indicating the number of possible configurations. Low entropy signifies a plethora of arrangements, whereas high entropy implies limited possibilities.
The combination of Efimov and Noether effects suggests that the potential arrangements of particles within a black hole could initially expand as they undergo black/white hole cycles. However, as the black hole's size is finite, the number of potential configurations will eventually decrease, indicating that a maximum level of information complexity will be reached.
One notable aspect of quantum mechanics is the principle that "what can happen, does happen," which can be viewed as a meta-Efimov effect. Each new Efimov effect could necessitate that it differs from prior combinations, requiring information about previous Efimov effects to be represented in the particles.
A sophisticated Efimov effect might create a new force that organizes content in such a manner that it illustrates the number of potential particle arrangements in a black hole over time, ultimately leading to increased complexity. Given the finite nature of black holes, a peak in information complexity will eventually be attained, potentially influenced by how past Efimov effects are represented in particles.
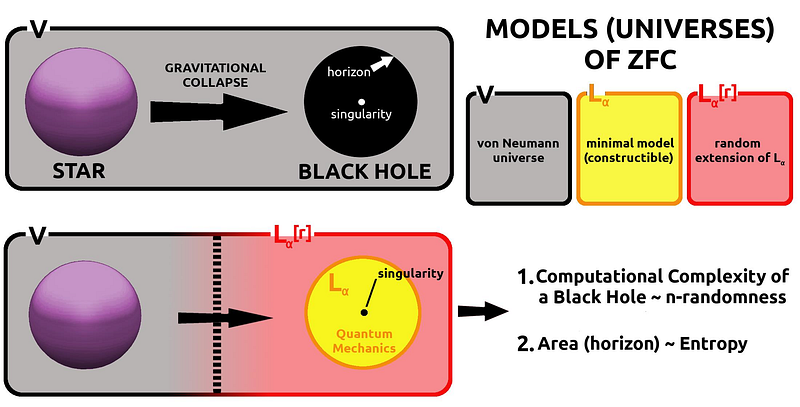
Chapter 3: The Second Law of Thermodynamics and Complexity
According to the second law of thermodynamics, the total entropy of an isolated system can only increase over time, reaching a state of maximum entropy if all processes are reversible. This concept is crucial when examining how to enhance mathematical complexity within a finite isolated system; the efficiency of information storage plays a critical role in determining the maximum complexity achievable.
In our universe, the ability to share videos online is possible due to efficient information storage methods. When sharing a video, only the changes between frames need to be communicated, rather than the entire content of each frame. This principle aligns with the idea that the second law of thermodynamics can foster complexity by promoting efficient information storage, thereby enhancing the capacity of a finite system to explore new mathematical complexities.
The emergence of new forces, such as temperature—an Efimov effect—can also facilitate increased mathematical complexity. For example, a gas at high temperatures exhibits greater complexity than one at absolute zero, as its temperature is directly tied to its capacity for reorganization and entropy.
Chapter 4: Quantum Complexity and Black Holes
Professor Leonard Susskind's research on the dynamics inside an AdS black hole reveals that the interior quickly attains thermodynamic equilibrium while simultaneously expanding in quantum complexity. Quantum complexity theory focuses on complexity classes defined by quantum computers, examining the challenges posed by computational problems within these classes.
Susskind identifies a correlation between the computational complexity of a quantum system and the positional entropy of a corresponding classical system. He suggests that the growth patterns of quantum system complexity parallel classical entropy growth.
My interpretation of Susskind's findings suggests that the anticipated growth of quantum system complexity relates to the expansion rate of our universe, driven by dark energy. Additionally, Kolmogorov complexity appears to be connected to gravitational forces. Understanding Kolmogorov complexity could provide insights into Newton's law of gravity and help clarify the phenomenon of dark matter.
In conclusion, if Susskind's research aligns with the mathematical concepts discussed here, it may necessitate revising Newton's law of gravity to account for information inherent in matter, including its history and temperature. Future articles will delve deeper into these ideas and explore their empirical testing, particularly in relation to the rotational velocities of stars in galaxies.