Notation in Mathematics

In mathematics, notation is crucial. While some argue that it shouldn't be, history has demonstrated its importance. For instance, Leibniz and Newton independently developed calculus, but Leibniz’s notation significantly simplified the subject, facilitating easier understanding and application, which ultimately led to its widespread adoption.

This historical debate over notations between Great Britain and Europe is a separate topic, but it illustrates the significance of notation in mathematical discourse.

Sums of Consecutive Odd Numbers

I aim to present a well-known concept using a new notation that I find intuitive. For two natural numbers, ( m ) and ( n ) where ( m < n ), we can define a new term.

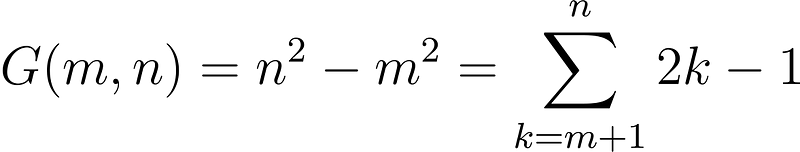
We shall call numbers of this form Goldbach numbers, a name that will become clear shortly.

As previously indicated, we can express ( G(m,n) ) in two forms: as a difference of squares or as a sum of consecutive odd numbers. For example, ( G(3, 8) = 8² - 3² = 7 + 9 + 11 + 13 + 15 = 55 ).

These numbers are remarkable because for each ( G(m, n) ), there exist natural numbers ( k ) and ( s ) such that ( G(m, n) = k cdot s ) and ( k + s = 2n ). In our example, ( G(3, 8) = 5 cdot 11 ) and ( 5 + 11 = 16 = 2 cdot 8 ).

This means ( G(m, n) ) provides both a factorization of ( G(m,n) ) and a partition of ( 2n ). This property stems from a geometric fact established by the Greeks centuries ago: ( n² - m² = (n + m)(n - m) ) and the sum of these two factors yields ( 2n ).

Interestingly, if ( 2n = k + s ) for some ( k ) and ( s ) in the natural numbers, there exists a natural number ( m ) such that ( G(m, n) = k cdot s ).

Proposition

For all natural numbers ( m < n ), there exist two natural numbers ( k ) and ( s ) such that ( G(m,n) = k cdot s ) and ( k + s = 2n ). Conversely, if ( 2n = k + s ) for some ( k ) and ( s ), there exists a natural number ( m < n ) such that ( G(m,n) = k cdot s ).

Proof

The first part is straightforward. For the second part, note that if ( 2n = k + s ), then ( k ) and ( s ) must be equidistant from ( n ) and lie on opposite sides of ( n ). This can be visualized as the intersection of a number line and a circle centered at ( n ) with a non-negative radius.

Assuming without loss of generality that ( k < n ) and ( s > n ), we can express ( k = n - m ) and ( s = n + d ) for some natural numbers ( m ) and ( d ). Thus, ( k + s = (n - m) + (n + d) = 2n + d - m ). Given ( k + s = 2n ), it follows that ( d = m ).

Consequently, we have ( k = n - m ) and ( s = n + m ) for some non-negative integer ( m ). This allows us to write ( k cdot s = (n - m)(n + m) = n² - m² = G(m, n) ), thereby proving the proposition.

Q.E.D.

Interesting Consequences

One immediate consequence of this proposition is that all numbers less than an even number ( 2n ) divide some Goldbach number ( 2n - 1 + 2n - 3 + ldots + 2m + 1 ).

Lemma 1

Let ( n ) be a natural number. For all natural numbers ( k < 2n ), there exists a natural number ( m ) such that ( k ) divides ( G(m,n) ).

Proof

Let ( k < 2n ). Then we can express ( 2n = k + s ). By our proposition, there exists ( m ) such that ( G(m,n) = k cdot s ).

Q.E.D.

A straightforward corollary follows:

Corollary

For every prime ( p < 2n ), ( p ) is a prime factor of some ( G(m,n) ).

With our notation established, we can now articulate a famous conjecture.

Goldbach’s Conjecture

For all natural numbers ( n > 1 ), there exists ( m < n - 1 ) such that ( G(m,n) = p cdot q ) for some prime numbers ( p ) and ( q ).

This statement is equivalent to Goldbach's conjecture, which asserts that every even number greater than 2 can be expressed as the sum of two prime numbers. The proof of this equivalence is as follows:

From our proposition, we know that there exist numbers ( k ) and ( s ) such that ( G(m,n) = k cdot s ) and ( k + s = 2n ). Since ( G(m,n) = p cdot q ), there can only be two such numbers, namely ( p ) and ( q ), which must also satisfy ( p + q = 2n ).

Conversely, if we find two prime numbers ( p ) and ( q ) such that ( 2n = p + q ), we again conclude from the proposition that there exists a natural number ( m ) such that ( G(m,n) = p cdot q ).

Thus, they are indeed the same statement expressed in our new notation. We can summarize:

For each ( n ), there exists ( m < n-1 ) such that ( G(m,n) ) is a semiprime.

It is essential to note that ( m < n-1 ) since if ( m = n-1 ), the proposition yields the factorization ( (2n-1) cdot 1 ) and the rather unremarkable sum ( 2n-1 + 1 = 2n ).

A consequence of this theorem is:

Lemma 2

Let ( m < n - 1 ) and ( G(m,n) = p_1 cdot p_2 cdot p_3 cdots p_L ) be the prime factorization of ( G(m, n) ). The sum of all the primes satisfies:

( p_1 + p_2 + ldots + p_L < 2n ).

Proof

By the proposition, we can group the primes in the factorization above into two groups: ( k = q_1 cdot q_2 cdots q_j ) and ( s = q_{j+1} cdot q_{j+2} cdots q_L ) so that ( G(m,n) = k cdot s ) and ( 2n = k + s ). Here, the ( q )s are simply permutations of the ( p )s.

Since ( m < n - 1 ), we can ensure ( k, s > 1 ). Thus, we arrive at:

( p_1 + p_2 + ldots + p_L geq q_1 cdot q_2 cdots q_j + q_{j+1} cdots q_L = 2n ).

Q.E.D.

This inequality arises from the fact that the product of natural numbers all greater than one exceeds or equals the sum of those numbers. When ( G(m,n) ) is a semiprime, the above situation becomes equality.

It’s evident from the definition that ( G(m, n) + G(n, k) = G(m, k) ), and generally, these numbers possess many more intriguing properties that I encourage you to explore.

I hope you found these elementary mathematical insights and puzzles enjoyable. Should you have any questions or comments, feel free to connect with me on LinkedIn.

For those interested in similar content, consider subscribing to Medium for complete access.