Chapter 1: Introduction to the Challenge

I am just hours away from completing my final exam for the second year of my mathematics course at university. Fingers crossed for a positive outcome! Let's take a moment to applaud this week's top performers in our math challenge:

1st Place: Carl Reiner Holdt with 7 Points 🌟 2nd Place: David Carnochan with 5 Points 🌟

Here’s the solution to our intriguing problem. We will explore how complex numbers can illustrate the path taken by a bee. The bee begins its journey at P0 = 0, making a 30-degree turn with each movement.

Chapter 2: Understanding Complex Numbers

In this case, z is expressed in the exponential format of a complex number. Generally, we can represent it as z = re^iθ in polar coordinates, where r indicates the distance from the origin and θ is the angle made with the real axis. Here, θ/6 corresponds to 30 degrees, while z illustrates the angle the bee turns.

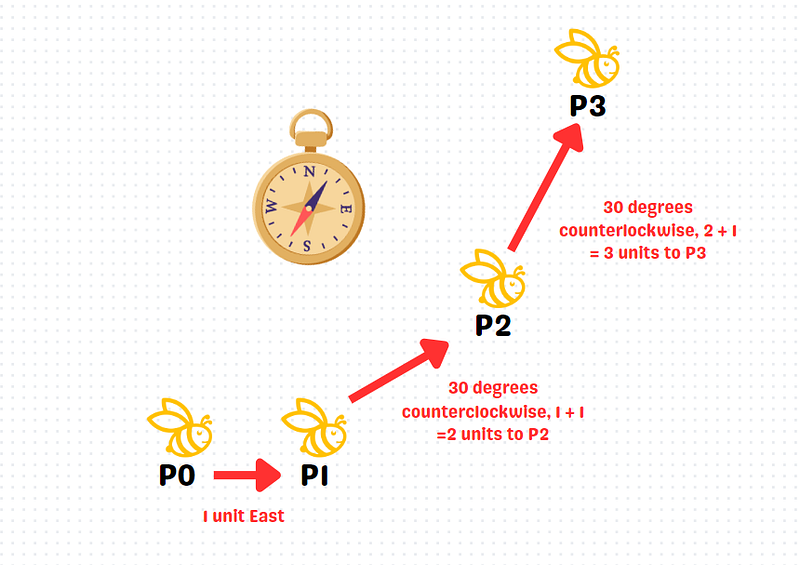
Let’s visualize this! The bee starts at point P0, moves 1 unit to P1, then turns 30 degrees clockwise and travels 2 additional units to P2. This sequence continues until she reaches P2015.

To analyze how far the bee has traveled upon arriving at any point Pj, we observe her movements:

• From P0 to P1: 1 unit, 30-degree turn.
• From P1 to P2: 2 units, another 30-degree turn.

Thus, the total distance from P0 to P2 is 1 + 2 = 3 units, and the total angle is 30 + 30 = 60 degrees. We can sum all integers from 1 to j to find the total distance traveled by the bee.

Notice that the bee turns 30 degrees only after covering the specified distance. Therefore, by the time she reaches Pj, she has turned (j - 1) times.

Chapter 3: Summation and Calculation

To solve this problem, we set j = 2015 and determine the sum:

There is significant algebra involved, so I’ll leave out some details. If you have insights on how to evaluate the sum, feel free to share in the comments!

The result should yield:

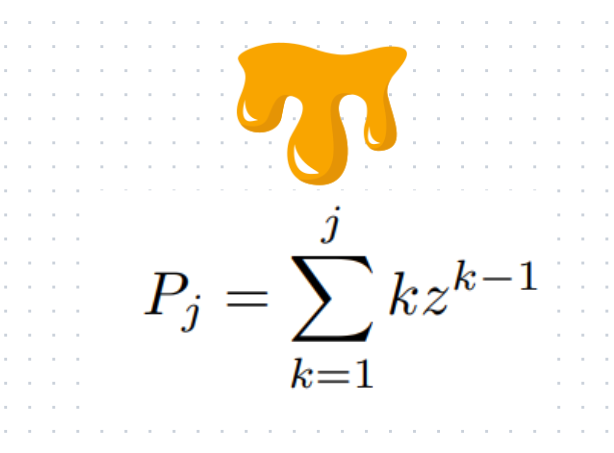
In this scenario, z = e^(iθ/6), indicating a complete rotation on the complex plane as z^12 = 1.

These relationships simplify the expression for P2015.

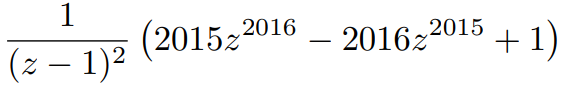
Now, let’s take a step back and review our goal.

The direction and magnitude of the arrow drawn from P0 to P2015 can also be represented as a complex number. Throughout this solution, P0 acts as the origin on the complex plane. The direction is determined by the argument of [z(z - 1)], while the length is defined by the magnitude of 2016/[z(z - 1)].

Substituting these values into P2015 gives us:

To resolve the puzzle, we compute 1008 + 6 + 1008 + 2 = 2024, leading us to the conclusion that the answer is B.

How did you fare in this week's Math Games? Looking forward to seeing you next week, challengers! 🌟

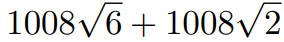
The first video, "The Flight Path of the Honey Bees," delves into the fascinating dynamics of how bees navigate their environments, using mathematical principles to elucidate their flight patterns.

The second video, "How Bees Fly" by Simon Rees, provides an engaging exploration of the mechanics behind bee flight, showcasing the intersection of biology and physics in their remarkable aerial abilities.