Understanding Stock Risk Through the Lens of the Sharpe Ratio
Written on
Chapter 1: Introduction to the Sharpe Ratio
In this chapter, we will delve into how to calculate the Sharpe Ratio, a well-regarded metric for assessing investment performance while factoring in risk.
"Between calculated risk and reckless decision-making lies the dividing line between profit and loss."
— Charles Duhigg, Pulitzer Prize-winning journalist
Start a conversation with your friends and family about stock market trading, and you may uncover varying perspectives on risk tolerance. You might discover three distinct profiles among them:
- Risk-averse individuals prefer certainty over potentially higher returns.
- Risk-neutral participants are indifferent to risk.
- Risk-seeking individuals are willing to accept significant uncertainty for the chance of substantial gains.
This framework is where the Sharpe Ratio becomes particularly valuable. It assesses investment performance by considering the associated risks.
How does it function? Here’s a brief overview of what we’ll cover:
- Definition of the Sharpe Ratio
- Utilizing functions and the pipe method to compute the Sharpe Ratio
- Comparing the Sharpe Ratio against competitors
- Important limitations of the Sharpe Ratio
- Conclusion
Section 1.1: Defining the Sharpe Ratio
Investors typically have two primary goals: maximizing investment returns while minimizing risk. The Sharpe Ratio provides a way to calculate risk-adjusted returns, offering a score that reflects this balance.
The formula is as follows:
Sharpe Ratio = (Rp — Rf) / Standard deviation
Where:
- Rp represents the expected or actual returns derived from historical data of the asset or portfolio.
- Rf indicates the risk-free rate, typically the returns on low-risk investments like U.S. Treasury Bonds.
- Standard deviation serves as a measure of risk; lower values indicate less volatility.
Interpreting the ratio: A Sharpe Ratio above 1 suggests that the investment is solid, with higher values indicating better performance.
Section 1.2: Calculating the Sharpe Ratio Using Python
To gather stock data, we will utilize the yfinance library, inputting the company's ticker and defining the periods for analysis. Here is what we aim to retrieve:
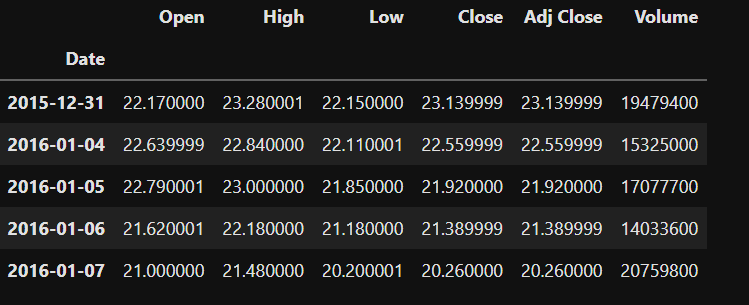
Disclaimer: The information in this blog post is intended for educational use only and does not constitute investment advice.
To determine the expected returns (Rp), we calculate the Compound Annual Growth Rate (CAGR), which reflects the annual growth of an investment over a specified timeframe:
CAGR = (EV/BV)^(1/n) - 1
Where:
- EV is the investment's ending value,
- BV is the investment's starting value,
- n is the number of investment periods.
We'll compute this using a series of functions chained together via the pipe method, which is a best practice recommended by Khuyen Tran, whose blog will be referenced at the end.
Subsection 1.2.1: Analyzing Twitter’s Investment Performance
Now that we have the CAGR for Twitter, we can display the result using the Tabulate library (refer to my previous post for instructions on how to use Tabulate).

Next, we will compute the standard deviation based on annualized volatility, which indicates the stock's price variation over time. A higher percentage signifies increased volatility (and risk). This is determined by annualizing daily returns through multiplication by the square root of 252 (the number of trading days).
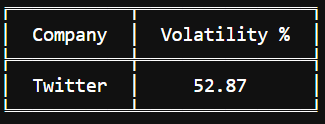
After establishing both the annualized volatility and CAGR, we need to determine the rf parameter, representing the risk-free rate. For this analysis, we will assume it to be 3%. Now, let’s calculate the Sharpe Ratio!

A Sharpe Ratio above 1 is deemed acceptable; however, Twitter’s stock shows a ratio of 0.09, indicating it is a risky investment with insufficient returns to justify its high volatility.
Chapter 2: Comparing Sharpe Ratios Among Competitors
Calculating Twitter's Sharpe Ratio is informative, but we must also compare it with its competitors to gauge its relative performance. Let’s now analyze the Sharpe Ratios for Meta (formerly Facebook) and Snap. Import their data using their respective tickers and apply the same calculations as before.
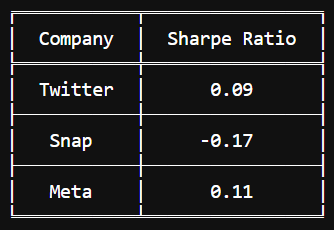
All calculated Sharpe Ratios are below 1, indicating unfavorable conditions. Twitter and Meta exhibit similar ratios, while Snap shows a negative Sharpe Ratio.
Section 2.1: Limitations of the Sharpe Ratio
It is crucial to note that the Sharpe Ratio has its limitations. It assumes that average returns follow a normal distribution, which is often not the case in financial markets. Returns frequently exhibit skewness due to unpredictable spikes and drops. Furthermore, the selected historical period can significantly influence the ratio, potentially skewing results based on the timeframe chosen.
Section 2.2: Conclusion
In summary, calculating the Sharpe Ratio using Python with functions and the pipe method has proven to be insightful. This metric is widely utilized due to its ease of calculation and interpretation. It serves as one of many tools for evaluating stocks and investments.
For a complete Jupyter Notebook with all the associated code, please visit my GitHub repository. If you found this article helpful, consider following me for more content, and connect with me on LinkedIn.
References:
- Python Clean Code: 6 Best Practices to Make Your Python Functions More Readable | by Khuyen Tran | Towards Data Science
- Sharpe Ratio Definition (investopedia.com)
Now, let’s enhance our understanding with some video insights.
This video, titled "The Sharpe Ratio: How to Evaluate Investment Performance with Risk in Mind Using Python," provides a thorough overview of the Sharpe Ratio and its importance in investment analysis.
In this video, "What is the Sharpe Ratio & How It Can Help Us Understand Risk Adjusted Stock Market Returns!" the concept of the Sharpe Ratio is further explored, highlighting its relevance to risk-adjusted returns in the stock market.