The Impact of Lady Muriel Bristol's Tea Experiment on Modern Science
Written on
Chapter 1: The Tea Party that Changed Science
In the summer of the 1920s, a group of scholars at Cambridge University gathered for a tea party. Among them was Sir Ronald Fisher, a prominent statistician, who offered a cup of tea to Lady Muriel Bristol. Unbeknownst to him, the way he prepared the drink would spark a significant debate. He poured the tea first, followed by the milk, to which Lady Muriel objected, insisting she could distinguish between the two methods of preparation.
Her assertion was not merely a matter of preference; she claimed to have a refined palate capable of detecting the difference. Fisher and his colleagues were skeptical, doubting anyone could possess such sensitivity. To settle the argument, they decided to conduct an experiment.
This paragraph will result in an indented block of text, typically used for quoting other text.
Section 1.1: Designing the Experiment
The team set up an experiment involving eight cups of tea, arranged randomly. Four cups had the tea poured first, while the other four had the milk added before the tea. Lady Muriel, unaware of which cups belonged to which group, was tasked with identifying the four cups prepared with milk first.
In this scenario, the null hypothesis posited that she could not tell the difference between the two groups. Notably, Fisher's design did not include an alternative hypothesis. The test statistic was based on the number of cups she correctly identified from the four prepared with milk first. Assuming the null hypothesis held true, they calculated the distribution of possible outcomes using combinations. There are 70 combinations for selecting 4 out of 8.

To determine the expected distribution if Lady Muriel could not distinguish between the cups, they needed to analyze the outcomes for every possibility:
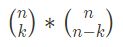
Here, n=4 represents the cups with milk first, and k symbolizes the number of correct identifications. From the 70 combinations, the expected distribution of correct guesses was as follows: 0 correct: 11, 1 correct: 162, 2 correct: 363, 3 correct: 164, and 4 correct: 1.
More broadly, the number of correct guesses (X) follows a Hypergeometric distribution:
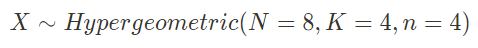
In applying the conventional probability criterion of p-value < 5%, it became evident that Lady Muriel would need to guess all four cups correctly to substantiate her claim of being able to discern the differences.
Section 1.2: Results of the Experiment
How did Lady Muriel fare in the experiment? According to David Salsburg, author of "The Lady Tasting Tea," she successfully identified all four cups. However, this result has been subject to some debate.
The more significant takeaway from this experiment is its endorsement of randomization in scientific studies. Deb Basu, an influential statistician, emphasized that this case represented "one of the two supporting pillars … of the randomization analysis of experimental data." Ultimately, this story illustrates how statistics transformed scientific inquiry, establishing it as an essential tool in our pursuit of knowledge.
Chapter 2: Understanding the Legacy
This episode, "The Experiment: The Lady Tasting Tea," delves into the historical significance of the experiment and its implications for modern statistical practices.
In "Fisher's Exact Test | Lady Tasting Tea," explore the statistical methods employed in the experiment and their relevance in today’s data analysis.
If you found this article engaging, you may also enjoy:
- Causal Inference: an Overview
- Hypothesis Testing: What It Is and How to Implement It in Python
Feel free to connect with me on LinkedIn if you'd like to discuss this topic further; I would be delighted to chat.