Unraveling the 2024 Bangladesh Mathematical Olympiad Problem 1
Written on
Understanding the Problem
In this discussion, we delve into a Diophantine equation featured in the 2024 Bangladesh Mathematical Olympiad. While it may initially appear daunting, there's no need for concern! Keep an eye out for potential shortcuts.
Initially, we observe that three of the terms in the equation are divisible by the product xy. What conclusions can we draw from this? Since both x and y are integers, the terms x³y, xy, and 2xy² being divisible by xy implies that x + y must also share this property. This insight significantly simplifies our task. But how can we leverage this condition effectively?
Given that xy divides x + y, it necessarily follows that xy must be greater than or equal to x + y. Thus, we have:
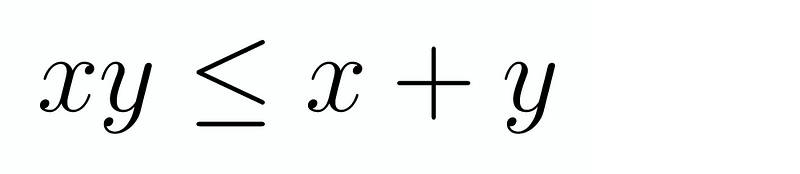
At first glance, this may not seem particularly beneficial. However, what if we could further constrain our findings? Specifically, let’s attempt to factor this expression in a more advantageous manner. We can rearrange it to form xy - x - y ≥ 0. This expression closely resembles (x-1)(y-1), albeit missing a constant. This is perfectly acceptable, as it indicates that our left-hand side equals (x-1)(y-1) - 1. Therefore, we have:
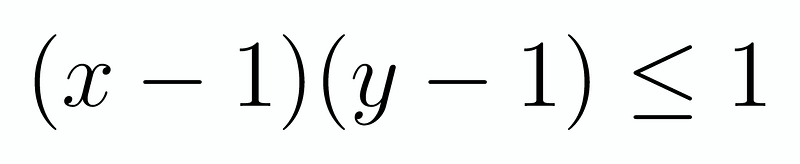
If x and y were to vary freely among all integers, this approach would be ineffective, allowing the left-hand side to take on arbitrary values. However, since we are limited to positive integers, the variables x and y can only take on three possible values: 0, 1, or 2.
Returning to our initial equation, let's consider the case where x = 0. In this scenario, it necessarily follows that y must also equal 0. Now, if we take x = 1, then y must divide y + 1, which leads us to the only feasible solution y = 1, validating our equation. Finally, for x = 2, we require that 2y divides 2 + y. This results in two possibilities for y: either y = 0 or y = 2. Here, only y = 2 satisfies our equation, confirming our solution.
Consequently, our three valid solutions are (x, y) = (0, 0), (1, 1), and (2, 2), and these represent all possible solutions.
Did you enjoy this analysis? If so, please consider supporting my work; your encouragement means a lot!
If you discovered an alternative solution, feel free to share your thoughts in the comments below!
Further Insights into Olympiad Problems
The second video titled "Bangladesh Mathematical Olympiad, higher level, 2023, problem 1" presents an in-depth examination of a challenging problem, offering valuable techniques for solving higher-level mathematical challenges.