Avoid Relying Solely on Hints: Embracing Alternative Solutions
Written on
Chapter 1: The Problem with Hints
Hints can sometimes lead you astray, diverting your attention from potentially more effective or faster methods for solving problems. Recently, I was working on a math exam question designed for exceptionally capable high school students. The question included a hint suggesting a particular approach.
After some reflection, I realized I could solve the problem more easily by disregarding the hint. I imagined myself as an eager 18-year-old student aiming to excel in the exam. How many students would feel confident enough to ignore the hint and pursue their own method? Likely, not many.
This serves as a reminder that hints often represent just one individual's method for addressing a problem, and there could be other, perhaps superior, ways to approach it. Let's examine the question further.

Sixth Term Examination Paper, Mathematics, 1991, Q4: Disregarding the Hint
The hint suggests we concentrate on the area that the guard cannot observe. However, let’s consider the perspective of the guard. As he moves back and forth from point A to point E, what can he see? Below is an alternative representation of the diagram:

I’d like to highlight a couple of simple points: The guard will always see the blue shaded region, regardless of his location along AE. This area totals 12?4 + 8?4 = 80 square units. Additionally, triangles A and B will be visible to the guard, varying with the position x. At one extreme — x = 4 — triangle B becomes degenerate (its area is zero).
Thus, our task simplifies to examining the areas of triangles A and B to determine when their combined area reaches a maximum and minimum. This simplification is likely overlooked if a student follows the given hint.
Finding the Sum of the Areas
We can utilize fundamental trigonometry for this. Below is another version of the diagram:

By determining the values of y and z in relation to x, we can formulate an expression for the total area of triangles A and B. Notably,
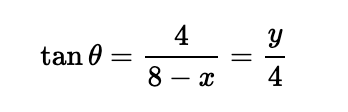
Thus, y = 16/(8-x), leading to the area of triangle A being 0.5 * 4 * y = 32/(8-x). Similarly:
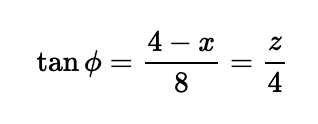
So z = (4-x)/2, and the area of triangle B is 0.5 * 4 * (4-x)/2 = 4-x. Therefore, we can express the sum of the areas of triangles A and B — which we will denote as Q:
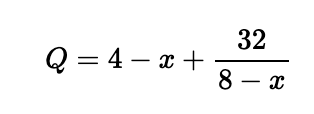
Finding Maximum and Minimum Values
Now we can proceed to find the critical points. This is a continuous function defined over the interval [0, 4], so we will differentiate it to locate turning points.
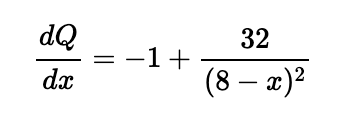
Setting this derivative to zero reveals that turning points occur when (8 — x)² = 32. Therefore, x = 4(2 ± √2). The only valid solution within our interval [0, 4] is x = 4(2 - √2).
The second derivative is
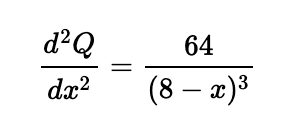
This is evidently positive at x = 4(2 - √2), indicating a minimum point.
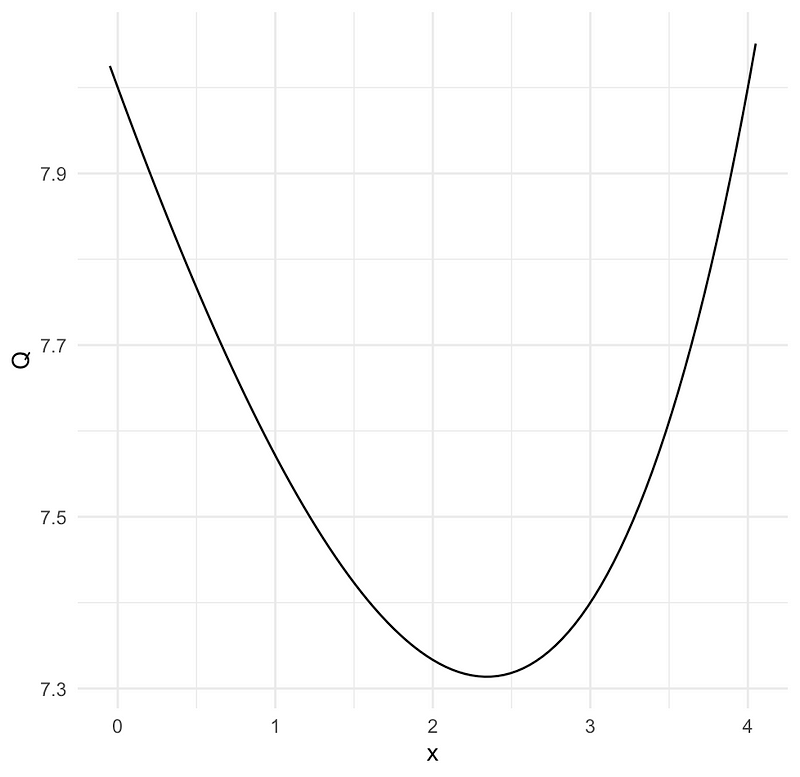
Since Q is continuous over the interval [0, 4], we know its value must increase from the minimum to both ends of the interval. We can confirm that at x = 0 and x = 4, Q = 8, making both points local maxima.
In conclusion, the guard has a maximum visibility of 88 square units when positioned at points A or E, and a minimum visibility of 80 + 4(2√2 - 1) square units when standing at a distance of 4(2 - √2) units from A.
A quick graphical representation of Q between x=0 and x=4 using R confirms our findings:
What are your thoughts? Did this approach simplify the problem compared to the hint provided? Feel free to share your insights!
