Unraveling the Last Coconut Puzzle: A Test of Intuition
Written on
Chapter 1: Introduction to the Last Coconut Puzzle
The Last Coconut Puzzle is an engaging challenge that examines your decision-making instincts. My inspiration for this write-up stemmed from Leonardo Barichello’s fascinating work on the subject.
Imagine yourself on a dream vacation at sea. Unfortunately, your ship encounters a mishap and sinks, leaving you as the sole survivor. Fortunately, you manage to reach a deserted island, but you soon realize you are utterly alone.
After searching the island for food, you spot a tempting coconut. Given your hunger, it feels like a gourmet feast in your current situation. As you excitedly approach the coconut, a monkey swings down from a tree, exclaiming:
“Beware, traveler! That coconut is mine. If you want it, you must challenge me in a game and win.”
Taken aback, you listen as the monkey lays out the game’s rules.
Section 1.1: Game Rules Explained
The monkey reveals two fair dice and explains how the game works:
- If the highest number showing on either die is 4 or less, you win.
- If the highest number is 5 or 6, the monkey wins.
- If both dice show the same number, the round is a draw.
- The winner will be determined by the best of three rolls.
- Should you win, the coconut is yours. If not, you become the monkey’s servant.
Given these high stakes, would you risk it? What do you believe your chances of winning are?
The first video titled "The Monkey and the Coconuts Puzzle" delves into the intricacies of this game, exploring the probabilities and strategies involved.
Section 1.2: Analyzing the Odds
Spoiler Alert: If you wish to solve the puzzle independently, consider pausing here.
Many assume the odds favor them, thinking the monkey has less chance of winning. However, the closed nature of this puzzle allows us to calculate exact probabilities.
First, envision all possible outcomes. With two fair dice, there are 36 potential results. Among these, 6 scenarios lead to a draw.
The outcome table illustrates the scenarios:

To find the winning outcomes for you and the monkey, we can label the players. For instance, if the result is (1, 4), Player 1 (you) wins, whereas (1, 5) means Player 2 (the monkey) wins.
The complete game outcome table looks like this:
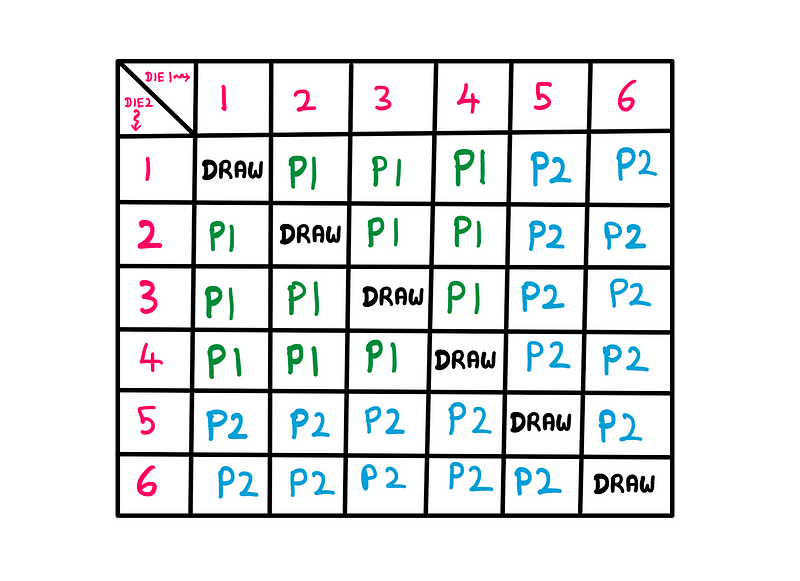
Counting the scenarios reveals that you win 12 out of 36 times, while the monkey wins 18 out of 36.
Using probability, we can state:
Probability of winning = 12/36 = 1/3 (approximately 33%).
Conversely, the monkey’s winning probability is 18/36 = 50%. This clearly indicates that the monkey holds the advantage in this game, attempting to ensnare you into servitude!
Chapter 2: Final Thoughts on Probability
One common error in understanding probability is conflating it with certainty. Just because you have a lower chance of winning does not guarantee loss. This randomness is what makes the game intriguing.
If the monkey proposed a “best of a million” scenario, the probabilities would lean closer to certainties. I’ve elaborated on the concept of expected value in my other work, which may be of interest to you.
The second video, "Intelligent Trader With 3 Sacks and Coconuts Puzzle," further explores these ideas in the context of strategic decision-making.
I hope you enjoyed tackling this puzzle. Stay tuned for more engaging challenges in the future!