# Understanding Linear Regression in Machine Learning
Written on
Chapter 1: Introduction to Linear Regression
Linear regression is a core supervised learning technique in the realm of machine learning. It serves to illustrate the connection between a dependent variable, often referred to as the target or response variable, and one or more independent variables, commonly known as predictors or features. The primary aim of linear regression is to identify the optimal line that embodies the linear correlation between these variables.

The standard representation of a linear regression model can be expressed as:
y = b0 + b1x1 + b2x2 + … + bn*xn
Where:
- y denotes the dependent variable.
- x1, x2, …, xn signify the independent variables.
- b0, b1, b2, …, bn are the coefficients (or weights) that we aim to estimate.
The coefficient b0 indicates the y-intercept, which shows the value of y when all independent variables are set to zero. Meanwhile, coefficients b1, b2, …, bn reflect how y changes with a one-unit shift in their respective independent variables, assuming other variables remain unchanged.
The fitting process for a linear regression model involves determining the coefficient values that reduce the discrepancy between the predicted and actual values of the dependent variable in the training dataset. This is typically achieved through a method known as ordinary least squares (OLS), which aims to minimize the sum of squared differences between these values.
Once trained, the model can be utilized for predicting outcomes on new data by substituting the independent variable values into the equation. It is crucial to mention that linear regression presupposes a linear relationship between the independent and dependent variables. If the correlation is non-linear, alternative methods such as polynomial or nonlinear regression may be more effective.
Additionally, there are various adaptations of linear regression, including multiple linear regression (for multiple independent variables), ridge regression (to address multicollinearity), and logistic regression (for binary classification tasks).
To deepen our understanding of linear regression, let’s explore some examples and key concepts.
Example 1: Predicting House Prices
Consider a scenario where we aim to estimate the selling price of houses based on their sizes (measured in square feet). Our dataset includes relevant information:
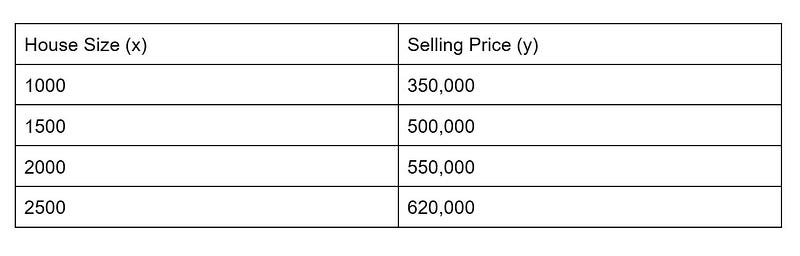
To conduct linear regression, we fit a line that accurately depicts the relationship between house size (x) and selling price (y). Our goal is to find the coefficients b0 and b1 that minimize the variance between the predicted and actual selling prices. The linear regression equation for this case would be:
y = b0 + b1*x
The objective is to estimate the coefficients b0 and b1. Once we have these values, we can predict the selling price of a new house based on its size.
Example 2: Multiple Linear Regression in Education
Now, let’s examine a multiple linear regression scenario where we wish to predict a student’s final exam score based on their study hours and the number of prior exams they have taken. The dataset includes:
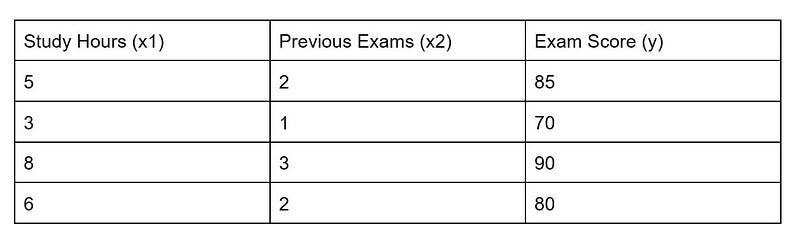
In this case, the multiple linear regression equation is represented as:
y = b0 + b1x1 + b2x2
Here, b0 is the y-intercept, b1 corresponds to study hours (x1), and b2 relates to the number of previous exams taken (x2). The aim is to estimate the values of b0, b1, and b2 that minimize the differences between the predicted and actual exam scores.
Assumptions of Linear Regression
Linear regression is built on several assumptions regarding the data:
- Linearity: A linear relationship should exist between independent and dependent variables.
- Independence: Observations must be independent.
- Homoscedasticity: The variability of residuals should remain constant across all independent variable levels.
- Normality: Residuals should follow a normal distribution.
- No multicollinearity: Independent variables should not be highly correlated with one another.
If these assumptions are not met, the linear regression model may yield inaccurate results. There are various diagnostic tools and remedies to address these violations and enhance the model's accuracy.
Evaluation Metrics for Linear Regression
To assess the performance of a linear regression model, several metrics can be employed, including:
- Mean Squared Error (MSE): This metric quantifies the average squared difference between predicted and actual values.
- R-squared (R²) Score: This indicates the proportion of variance in the dependent variable that can be explained by the independent variables.
- Residual Analysis: Evaluating the residuals can uncover patterns or assumption violations in the model.
Stay tuned for my next post, where I will delve into these metrics in detail!
I hope this article has clarified your understanding of linear regression concepts. If you found it beneficial, please consider following me on Medium, liking, and sharing it with others to help expand my reach.
Did you enjoy this article? If so, please support me by liking and sharing it with your friends, and don't forget to follow me on Medium for more insightful articles!
Feel free to leave any questions in the comments, and I will ensure that I respond to each one of you.
I’m excited to share my latest web application, built with Angular, Spring Boot, Firebase, Docker, and Kubernetes! Explore Stockify for more details.
Curious about my ongoing projects? Visit my Personal Website and GitHub for updates.
If you'd like to connect, please reach out on LinkedIn.
Chapter 2: Further Insights into Linear Regression
In this chapter, we will explore two informative videos that enhance our understanding of linear regression:
The first video titled "Why Linear Regression for Machine Learning?" provides an overview of the significance of this algorithm in machine learning.
The second video, "Stanford CS229: Machine Learning - Linear Regression and Gradient Descent | Lecture 2 (Autumn 2018)," offers an in-depth lecture on linear regression and gradient descent methods.