Revolutionizing Adaptation of Large Language Models with LoRA
Written on
Chapter 1: Understanding the Shift in Language Model Adaptation
The advent of BERT in 2019 marked a significant turning point in the adaptation of large language models (LLMs) for various tasks. Traditionally, fine-tuning was the go-to method for this purpose. However, the introduction of LoRA (Hu et al. 2021) has fundamentally transformed this approach by demonstrating that the weight update matrix can be substantially simplified through low-rank factorization, often resulting in a dramatic reduction in trainable parameters.
LoRA has gained immense traction in the NLP community due to its ability to quickly and efficiently adapt LLMs to specific tasks while maintaining a smaller model size than previously possible.
The Challenges of Fine-Tuning
BERT's introduction revolutionized NLP by establishing the pre-training and fine-tuning paradigm. After undergoing unsupervised pre-training on vast amounts of text data, BERT could be fine-tuned on particular tasks using minimal labeled data, owing to its prior learning of general linguistic patterns. This method set a standard practice within NLP.
However, as LLMs have grown exponentially larger, the challenges associated with fine-tuning have escalated. For instance, while the BERT-Base model contained a relatively modest 110 million parameters, today’s models like GPT-3 boast an astonishing 175 billion parameters. This presents significant engineering hurdles since deploying a fine-tuned model requires storage equivalent to the original pre-trained model. For example, a 175 billion parameter model utilizing 32-bit precision necessitates approximately 650GB of storage — a daunting figure considering that NVIDIA's H100 GPU has only 80GB of memory.
In the initial BERT paper, the authors claimed that fine-tuning was “straightforward.” However, this assertion may not hold true in the context of today's model sizes.
Enter LoRA
Neural network weights can be thought of as matrices, which means that the updates to these weights during training also form matrices. For instance, a neural network with two fully connected layers of 1024 neurons each would generate a 1024x1024 weight update matrix.
The core premise of LoRA is that the weight update matrices during LLM fine-tuning exhibit low intrinsic rank.
To elaborate, a matrix with low intrinsic rank can be represented with fewer parameters. For example, a 1024x1024 matrix with a rank of 10 can be reconstructed as the product of a 1024x10 matrix and a 10x1024 matrix, leading to a significant reduction in parameters (from 1 million to 2,000). This process is known as low-rank factorization.
The lower the intrinsic rank of a matrix, the more redundant information it contains, allowing for more aggressive compression through low-rank factorization, with the lowest possible rank being 1 (the product of two vectors).
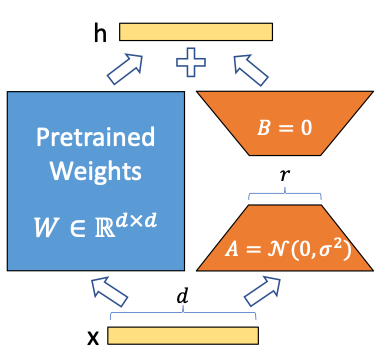
LoRA simplifies the weight update matrix ?W by approximating it with low-rank factorization: ?W = AB, where A and B are the low-rank matrices and r is the rank, a hyperparameter that can be adjusted. This means that during inference, we only need the frozen pre-trained weights W alongside the smaller matrices A and B to make predictions: y = Wx + ABx.
Advantages of LoRA
LoRA presents numerous advantages over traditional fine-tuning:
- Speed: Instead of training billions of weights, only the A and B matrices are learned, which are significantly smaller and faster to adapt. Research using GPT-3 indicates that LoRA is 25% quicker than standard fine-tuning.
- Task-switching: In conventional fine-tuning, each task necessitates a complete set of fine-tuned weights. LoRA, however, requires only the pre-trained weights and one set of low-rank matrices per task, facilitating quick transitions between tasks.
- Reduced Overfitting: The number of parameters learned in LoRA is typically much smaller than in traditional fine-tuning, lowering the risk of overfitting.
- Smaller Model Checkpoints: This allows for more frequent logging of checkpoints, enabling techniques like checkpoint averaging. For instance, utilizing a rank of 4 reduces GPT-3's size from 350GB to just 35MB.
- Stability: Results obtained via LoRA are consistently stable across different runs, unlike fine-tuning, which can be erratic, often requiring multiple runs with varying seeds to find the best outcome.
Which Weights Does LoRA Adapt?
In a Transformer block, which serves as the foundation for modern LLMs, LoRA can be applied to various components, including multi-head attention layers (key, query, and value matrices), Feed Forward MLP layers, Add & Norm layers, linear projection layers, and Softmax layers, along with their corresponding biases.
Where Should LoRA Be Implemented?
The original LoRA study focused on applying LoRA solely to the attention layers while freezing the rest of the model for efficiency. While this method is parameter-efficient, it might not yield the best performance.
The authors suggest that training the bias terms alongside the LoRA matrices can enhance performance without significantly increasing parameter count. Research by Sebastian Raschka indicates that applying LoRA across all weights in a Transformer model may yield accuracy improvements of 0.5-2%, depending on the specific task.
In summary, while limiting LoRA to attention weights conserves parameters, extending its application to the entire model can enhance performance, albeit at the cost of additional parameters.
How Does LoRA Perform?
The authors tested LoRA across various LLMs, including Roberta-Base, Roberta-Large, Deberta-XXL, GPT2-Medium, GPT2-Large, and the largest, GPT-3. In all cases, they replaced the attention layers with LoRA with a rank of 8, consistently finding that performance was either on par or exceeded that of traditional fine-tuning, all while drastically reducing the number of trainable parameters.
Notably, the LoRA model for GPT-3 reduced the number of trainable parameters from 175 billion to just 4.7 million, achieving a remarkable reduction of five orders of magnitude while also improving accuracy by 2% on the MNLI-m dataset compared to fine-tuning.
Let that resonate: a 2% increase in accuracy alongside five orders of magnitude fewer trainable parameters showcases the extraordinary low-rank nature of the weight update matrix.
How Low-Rank Can We Go?
Astonishingly, LoRA remains effective even with very low values of rank r, such as 4, 2, or even 1, where the weight update matrix can be expressed with just a single degree of freedom, similar to collaborative filtering. In experiments with the WikiSQL and MultNLI datasets, no significant performance differences were observed when reducing rank from 64 to 1.
Nonetheless, the minimal achievable rank in LoRA is likely contingent on the complexity of the downstream task relative to the pre-training task. For instance, adapting a language model for a different language than the one it was originally trained on may necessitate a higher rank.
In essence, a practical guideline could be: the simpler the fine-tuning task and the closer it aligns with the pre-training task, the lower the rank can be without sacrificing performance.
A New Paradigm Shift in NLP
LoRA paves the way for quicker, more robust adaptations of pre-trained LLMs to specific tasks, utilizing significantly fewer learnable parameters than traditional fine-tuning. This innovation is particularly beneficial for machine learning applications involving very large LLMs that need to be fine-tuned for various tasks, such as e-commerce, where product descriptions must be classified according to diverse regulations.
The success of LoRA highlights the surprisingly low rank of weight updates during fine-tuning, with some cases achieving as low as r=1. This raises intriguing questions regarding the implications of this finding. For instance, consider a scenario with four neurons fully connected to four others, represented by a 4x4 weight matrix. In the most extreme case, we could express updates to this matrix as the outer product of two 4-dimensional vectors that encapsulate changes in all weights associated with a specific neuron.
This insight is crucial for understanding the low-rank nature of fine-tuning: weights undergo broad, coarse updates rather than localized, intricate adjustments. To draw a loose analogy, the model doesn't genuinely "learn"; rather, it retains information.
Moreover, it is intuitive that the lowest feasible rank is influenced by the difficulty of the fine-tuning task in relation to the pre-training task. For example, fine-tuning an LLM in a language different from its pre-training language likely requires a larger rank to achieve satisfactory results. It would be valuable to investigate how the minimum rank shifts based on the depth of Transformer blocks, as I anticipate lower ranks in the early layers (which change less) and higher ranks in the later layers (which change more).
LoRA has the potential to redefine the landscape of NLP, and we are just beginning to witness its full impact on the broader machine learning field.
The first video titled "10 minutes paper (episode 25): Low Rank Adaptation: LoRA" offers an insightful overview of LoRA's mechanisms and implications in language model adaptation.
The second video, "Adam Zíka: Low‑Rank Adaptation (LoRA) in Large Language Models," delves deeper into the application of LoRA in large-scale language models, presenting experimental results and practical insights.