Bayesian Fundamentals

To grasp this argument, we must familiarize ourselves with the basics of Bayesian analysis. We denote P(A|B) as the probability of event A being true, given that B is true. A familiar illustration of this is in the context of medical testing: A represents the event of having a disease, while B indicates testing positive for that disease.

Due to the possibility of false positives, P(A|B)—the probability that you have the disease after a positive test—is not guaranteed to be 100%.

Bayes' Theorem provides a framework for calculating such probabilities:

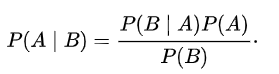
In this context, I’ll refer to P(A) as the prior probability, representing our belief in the truth of A before considering the new evidence B. For instance, what is the likelihood that you have the disease before knowing the test results?

Bayes' Theorem is a universally accepted mathematical principle, yet it often yields surprising results that may seem counterintuitive. We should trust these outcomes, as humans are notoriously poor at assessing probabilities.

For example, consider a disease test with a 99% accuracy rate, implying a 1% chance of both false positives and false negatives, with the disease's prevalence being just 0.5%. A positive test might lead you to believe there's a 99% likelihood of having the disease, but upon applying the numbers, you would find your actual probability of having the disease is only about 33%. A competent physician would likely recommend a retest, recognizing the high probability of a false positive.

The surprising aspect here is that Bayes’ Theorem factors in our prior knowledge regarding the disease's rarity, which significantly influences the probability calculation.

A Practical Illustration

Let's illustrate this with a straightforward example: Imagine a large container filled with golf balls, where the contents are not visible. The number of balls could range from one to a million, but we know that at some point, a red ball was dropped in, while the rest are standard white golf balls.

In our experiment, we draw balls sequentially until we find the red one. For instance:

• First draw: white
• Second draw: white
• Third draw: red

After this, we want to apply Bayesian methods to determine the likelihood of there being three, seven, or even a million balls in the container, given that we drew the red one on our third attempt.

In probabilistic terms, we need to evaluate the probability of x balls being in the container, given that the red ball was drawn on the third try. This situation calls for Bayes' Theorem.

Let A? represent the hypothesis of having exactly i balls in the container. We assume all scenarios are equally probable, meaning P(A?)=1/100 for all i. Using Bayes’ Theorem, we can compute:

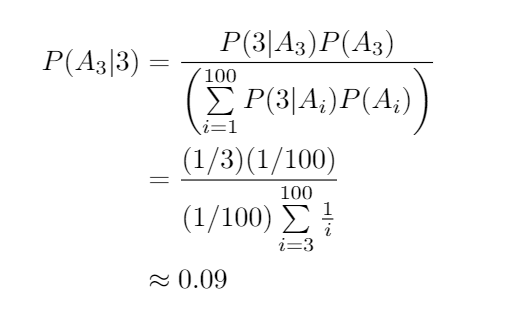
This calculation may seem complex, but it primarily involves substituting values into Bayes' Theorem. Note that P(3|A?)=0 because the chance of drawing the red ball third, given only one ball exists, is zero.

If the container has a maximum capacity of 100 balls, our experiment shows roughly a 9% likelihood that there are exactly three balls in the container.

Interestingly, as we increase the assumed total number of balls beyond three, the probability of that assumption being correct decreases, which is entirely logical. If there are indeed 100 balls, it seems improbable to draw the red ball so early.

Evaluating the Example

There are various ways to analyze this scenario. If the container could hold millions of balls while maintaining a uniform prior distribution, the overall probabilities would diminish, yet the general trend would remain consistent.

It becomes increasingly unreasonable to assume a large number of balls exists when we find the red one early in the sequence. If there were a million balls, the odds of drawing the red ball as the third would be exceedingly low. Conversely, if only five balls were present, drawing the red ball third wouldn’t be surprising.

You might also focus solely on this “earliness” concept and reformulate the calculations to assess the probability of A? based on finding the red ball by the third draw. This approach is common in discussions surrounding Doomsday arguments, and while more intricate, the same principle applies.

The complexity arises from trying to derive a distribution over natural numbers, but a simplified comparison between two options—“small total number of balls (e.g., 10)” versus “large total number of balls (e.g., 10,000)”—yields a striking result: approximately a 99% chance that the “small” hypothesis is valid.