Chapter 1: Introduction to the Problem

Recently, I was approached by a high school student who was struggling with a mathematical problem given by his teacher. After weeks of effort without success, he sought assistance. As many of my regular readers might know, I am always eager to engage with challenging problems, so I was glad to take a look at this one.

The problem consists of two parts: the first requires sketching the graph of a specific function, and the second asks us to demonstrate that the integral of this function over the positive x-axis falls between 0 and 1.

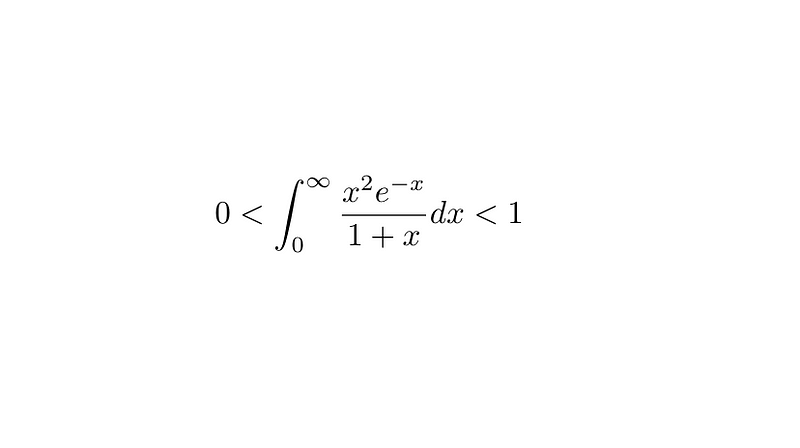
Chapter 2: Sketching the Graph

To sketch the graph of a non-trivial function, it’s essential to begin with several key questions:

• Are there any stationary points, such as turning points or inflection points?
• What are the behaviors of the function as x approaches ±∞?
• Are there any points where the function is undefined, potentially indicating asymptotes?

Let's start with identifying the turning points. We can apply the quotient rule for differentiation:

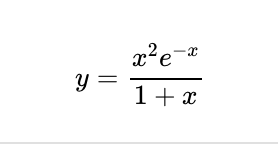
This allows us to find that the derivative, dy/dx, equals zero at three values of x: x = 0 and x = ±√2. These points are crucial for our graph's behavior.

To classify these stationary points as local maxima, minima, or inflection points, we can either compute the second derivative or analyze the changes in the function’s value around these points.

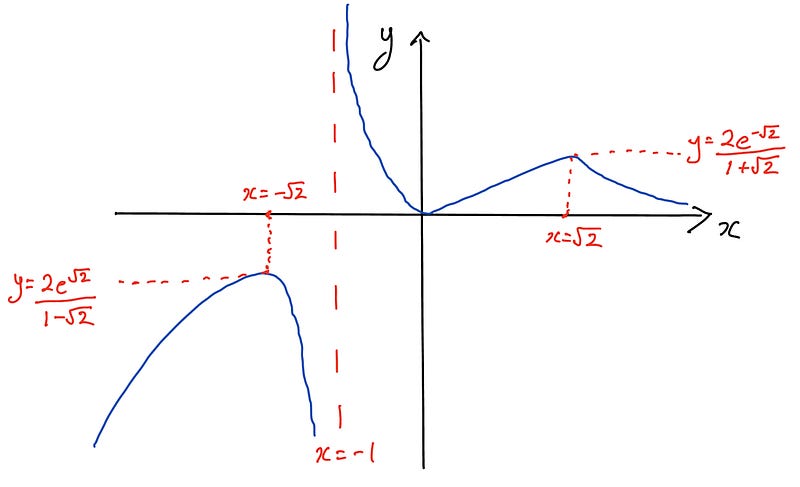
• At x = 0, we observe that y = 0. For -1 < x < 0, y is positive, and similarly, for 0 < x < 1, y remains positive. Therefore, we conclude that x = 0 is a local minimum.
• For x = √2, since y is positive, the function increases from x = 0 to x = √2. Beyond x = √2, y approaches zero, indicating a local maximum.
• At x = -√2, the value of y is negative. Additionally, there's an undefined point at x = -1, where y approaches positive infinity from the right and negative infinity from the left, confirming an asymptote.

Here’s a rough sketch of the curve based on this analysis:

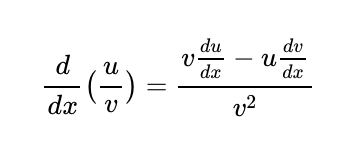
Chapter 3: Evaluating the Integral

Now that we have the graph, we can tackle the integral question. The integral represents the area under the curve, and for x > 0, it is evident that this area is positive. However, we still need to show that the integral is less than 1.

Let's consider the integral:

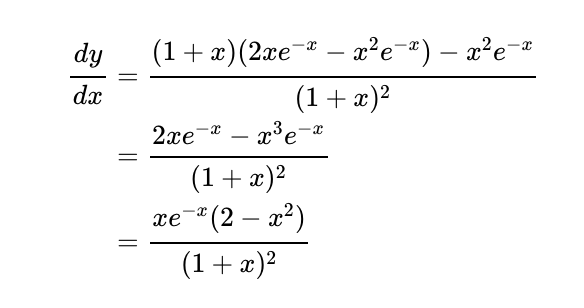
Initially, I attempted to apply standard integration techniques, but I quickly discovered that finding an exact value was complex and not necessary for our goal. Instead, I experimented with breaking the function into simpler components.

Note that:

The first term appears more manageable for integration, so I will use integration by parts:

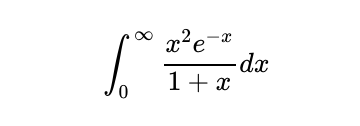
By letting v = x and du/dx = e^{-x}, we can proceed to evaluate:

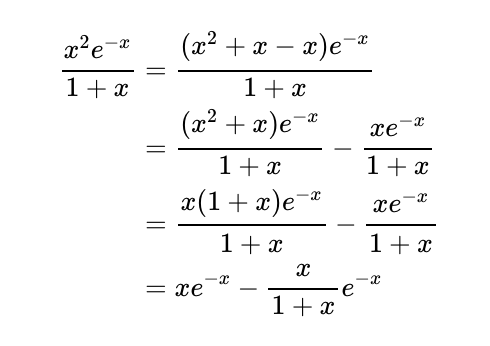
As x approaches infinity, the first term converges to zero. Evaluating at x = 0 also results in zero. The second term evaluates to -1. Thus, we conclude that:

For all x > 0, we can assert that:

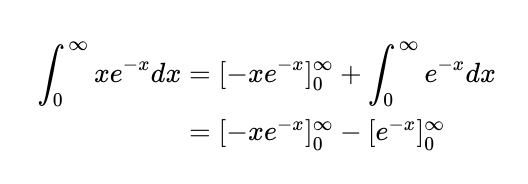
Finally, integrating leads us to:

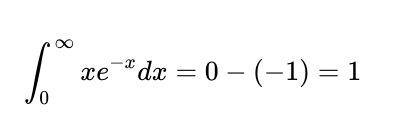
In conclusion, we can determine that the value of the integral lies between 0 and 1.

What are your thoughts on this approach? Would you have tackled it differently? I welcome your comments.

Chapter 4: Related Video Resources

In this video titled "The Hardest Integral I've Ever Done," the presenter dives into a particularly challenging integral, providing insights and strategies for tackling difficult integration problems.

This video, "Integrals - Most Difficult U-Substitution Problem," explores complex U-substitution techniques that can simplify challenging integral calculations.