Understanding the Dynamics of Pulley Systems in Physics
Written on
Chapter 1: Introduction to Pulley Systems
Pulley systems play a vital role in various applications, including elevators and weightlifting machines. They represent an elegant application of mathematical principles.

A pulley system consists of interconnected objects linked by inelastic cables or strings that traverse over smooth pulleys, typically wheels mounted on fixed axles. In our daily lives, we often encounter setups where two heavy objects are tied together by a sturdy cable. The cable loops over a smooth pulley positioned at the top, allowing the objects to move vertically on either side.
For instance, consider an elevator system where one side features the elevator, and the other side contains a counterweight. Similarly, in a weightlifting machine, a person pulls on a cable that moves over a pulley, counterbalanced by weights.
Mathematical modeling of pulley systems can be an intriguing challenge, especially using the mathematical concepts typically introduced in high school. I recently encountered an engaging problem that yielded a satisfying solution. To address this problem, we need to apply Newton's laws, basic motion equations, and some insights into energy and momentum. Additionally, a systematic approach is necessary for effective mathematical modeling.
Let’s outline the problem:
A piledriver consists of a mass M connected to a lighter counterweight m through a light, inextensible string that runs over a smooth, fixed pulley. Below the piledriver is a pile. When released from rest above the pile, the piledriver will collide with it, and the collisions are perfectly inelastic. Our goal is to demonstrate that the time taken for the piledriver to come to a stop is three times the time taken for it to strike the pile for the first time.
Understanding the Problem
Diagrams are incredibly helpful for visualizing mechanics problems. Below is my diagram illustrating the initial configuration, with the piledriver positioned above the pile.
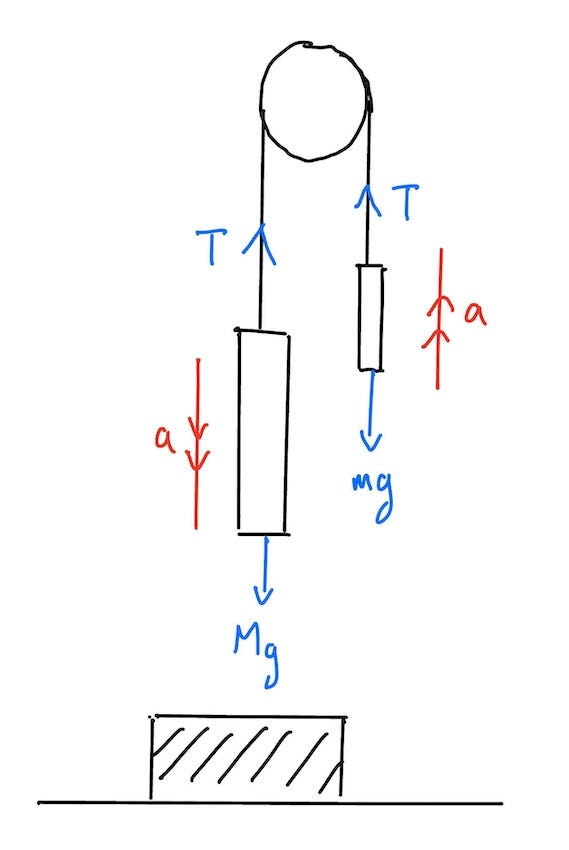
In this setup, we expect the piledriver to impact the pile upon release. The collision is deemed perfectly inelastic, implying that all kinetic energy is lost, and the piledriver remains stationary post-collision.
Nevertheless, the counterweight will continue to ascend after the collision, resulting in the string becoming slack until gravity halts the counterweight, prompting it to descend. The following diagram depicts this scenario:

At a certain point, the string will become taut again, leading to tension that pulls the piledriver upward until gravity brings it to a standstill. The piledriver will then fall until it collides with the pile again, repeating this cycle until the system reaches a permanent halt.
Examining Movement Prior to the First Collision
Upon release, a force acts on the system, causing it to accelerate. Let’s consider downward forces as positive and upward forces as negative. We can apply Newton's second law to derive simultaneous equations for both sides of the pulley, using g to denote gravitational acceleration:

By rearranging the second equation and substituting it into the first, we can derive an expression for the system's acceleration:
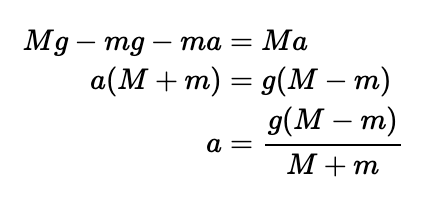
To continue, we need to express the time taken for the first collision. Using motion equations, we know the acceleration, and the initial velocity ( u = 0 ). Let’s denote the velocity at the collision point as ( v ). We can employ the equation ( v = u + at ) to find the time until the first collision:
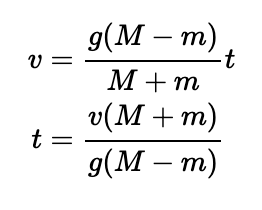
Analyzing Movement Between the First and Second Collisions
Immediately after the first collision, the piledriver remains stationary, while the counterweight continues to ascend against gravity until it comes to a halt and then descends.
At the moment of collision, the piledriver’s velocity is ( v ), meaning the counterweight also ascends at this speed. After the collision, the counterweight continues moving upward with initial speed ( v ) until gravity brings it to a stop. The time taken for this ascent is ( frac{v}{g} ), and thus, the total time for the string to become taut again is ( frac{2v}{g} ).
When the string becomes taut again, the tension will cause both the piledriver and counterweight to move together at a new velocity, denoted as ( v' ).
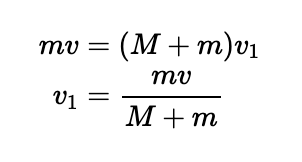
This system will decelerate due to gravity until it reaches velocity ( v' ) at the point of the second collision. We can use similar methods to calculate the time required for the piledriver to decelerate to a halt, where the initial velocity is ( v' ), final velocity is zero, and the acceleration is that of the entire system:
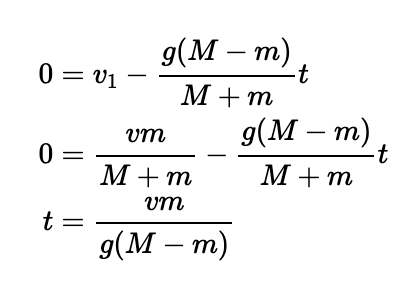
To find the total time ( T' ) between the first and second collisions, we must double this time and add it to the time taken for the counterweight to ascend and descend:

Exploring Movement Between Subsequent Collisions
Using the same logic, if ( v' ) is the system’s speed just before the second collision, then the counterweight will return to a taut string position in ( frac{2v'}{g} ). At this stage, we can express the new speed ( v' ) of the system as:
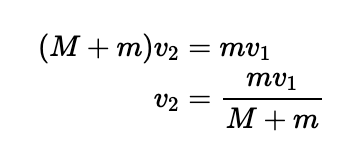
Employing similar techniques, we can calculate the time taken for the combined system to decelerate to zero:
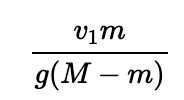
Following this method, we can deduce the time ( T'' ) between the second and third collisions:
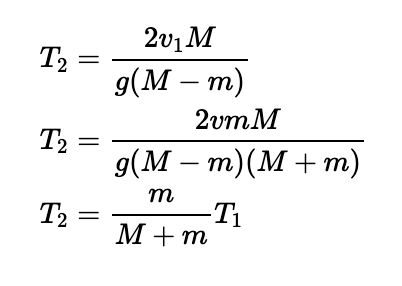
It becomes evident that the time intervals between collisions form a geometric sequence, specifically:

Finalizing the Calculation
Recognizing that our sequence of times between collisions behaves geometrically with a common ratio of ( frac{m}{M+m} ) and a first term of ( T' ), we see that since this common ratio is less than 1, the total time from the first collision until all subsequent collisions converge to a limit. We can compute the sum of this geometric series as follows:
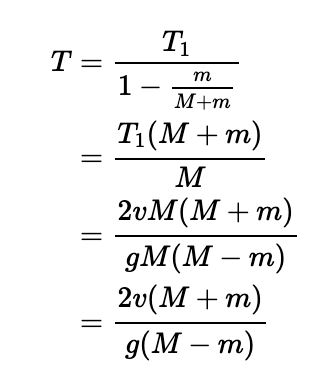
It’s crucial to note that this total time is equivalent to twice the time taken for the piledriver to impact the pile for the first time. Therefore, the complete duration required for the system to come to a halt is three times the time taken for the initial collision.
What are your thoughts on this problem? Would you have approached it differently? Feel free to share your insights!
Chapter 2: Practical Applications of Pulley Systems
This video, "How to make a Simple Pulley System," provides an excellent introduction to constructing a basic pulley system and demonstrates its applications.
The second video, "This is how simple pulley systems work - Rope Access Rigging," explains the mechanics of pulley systems in practical scenarios, enhancing understanding of their functionality.