Calculating Distances to Nearby Stars: Understanding Stellar Parallax
Written on
Chapter 1: The Quest for Cosmic Knowledge
For centuries, humanity has grappled with understanding our position in the universe. From the early applications of astronomical trigonometry in ancient civilizations like Babylon, Egypt, Greece, and the Islamic world, to the sophisticated astrophysical calculations of contemporary astronomers, the quest for our cosmic address has been relentless.
Trigonometry, a mathematical field examining the relationships between the angles and lengths of triangles, has roots tracing back nearly 5,000 years. Once viewed as a mundane branch of mathematics, it revolutionized scientific understanding and continues to play a crucial role today, albeit often unnoticed.
Section 1.1: Understanding Stellar Parallax
The concept of trigonometric parallax is essential for determining a star's distance from Earth. Parallax describes the apparent shift in an object's position relative to distant stationary objects based on the observer's perspective. For instance, if you extend your thumb in front of your face and switch between your eyes, your thumb appears to move against a fixed background. The extent of this movement is influenced by the distance between your eyes.
This principle can be applied to celestial bodies. By employing trigonometric functions, we can calculate the distance to relatively nearby stars, using more distant stars as stable reference points. However, stars located beyond approximately 100 parsecs (or 326 light-years) have parallax angles that are too minuscule to measure accurately from Earth's surface due to atmospheric disturbances. Nevertheless, distances to stars within this range can be effectively computed using ground-based telescopes. By observing a star's position six months apart, we can determine its parallax angle. Given that the distance from Earth to the Sun is one astronomical unit (AU, roughly 93 million miles), and knowing the angle of the star in relation to the vertical, we can use the tangent function to find the distance (tan = opposite/adjacent).
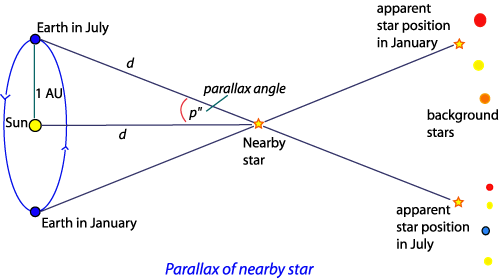
Section 1.2: Calculating Distances with Trigonometry
In the diagram above, the relationship can be expressed as: tan(p) = 1 AU / d, where the opposite side (p) equals 1 AU, and the adjacent side is d — the distance to the star. This equation allows us to calculate the distance: d = 1 AU / tan(p).
Trigonometric parallax is measured in arcseconds and parsecs, due to the minuscule shifts of stars. One arcsecond is 1/3600 of a degree, and one parsec is defined as the distance at which a star exhibits a parallax angle of one arcsecond. To find the distance of one parsec, we utilize the formula:
d = 1 AU / tan(1 arcsec)
Calculating this gives us:
d = 92,955,807.3 miles / tan(1/3600 degrees) = 19,173,511,582,127 miles * 1 LY/5.88 trillion miles = 3.26 LY.
In summary, 1 parsec equals 206,265 AU or 3.26 light-years.
Chapter 2: Proxima Centauri and Its Parallax
The closest star to our solar system, Proxima Centauri, has a parallax angle of 0.76813 arcseconds (a smaller angle indicates a greater distance).
To convert this angle into degrees:
0.76813 arcsecs * 1 degree/3600 arcsecs = 0.0002133694 degrees.
Using this value, we can calculate the distance to Proxima Centauri:
d = 1 AU / tan(0.0002133694 degrees) = 268,528.56835524 AU * 1 parsec/206,265 AU = 1.3 parsecs.
This translates to:
1.3 parsecs * 3.26 LY/1 parsec = 4.2 LY.
Thus, Proxima Centauri is approximately 1.3 parsecs or 4.2 light-years away from Earth.
A more straightforward method involves a direct relationship: d = 1/p, where the distance to a nearby star is equal to 1 AU divided by its parallax angle. This formula naturally yields a distance in parsecs, since one parsec corresponds to a star with a parallax angle of one arcsecond (1/3600 degrees) based on a baseline of 1 AU.
For Proxima Centauri:
d = 1 AU / 0.76813 arcsecs = 1.3 parsecs.
Trigonometry beautifully illustrates the precision inherent in mathematics and the fundamental structure of our universe. The enduring truth of trigonometric ratios and equations captures the very laws governing our reality, enabling us to comprehend Earth's relationship with other celestial bodies. These inquiries reflect the essence of human curiosity, and through the application of trigonometry, we can begin to uncover the mysteries of the cosmos.

In this video, we delve deeper into measuring distances to stars using the stellar parallax method, offering a comprehensive explanation of the process and its significance in astronomy.