An Alternative Method for Calculating Triangle Area
Written on
Understanding Triangle Area Calculation
Let’s consider a fundamental question: How do you determine the area of a triangle? A good starting point is to examine the area of a rectangle. Imagine a rectangle ABCD with sides measuring 'a' and 'h'. To find its area, you would multiply the base by the height: Area = a × h.
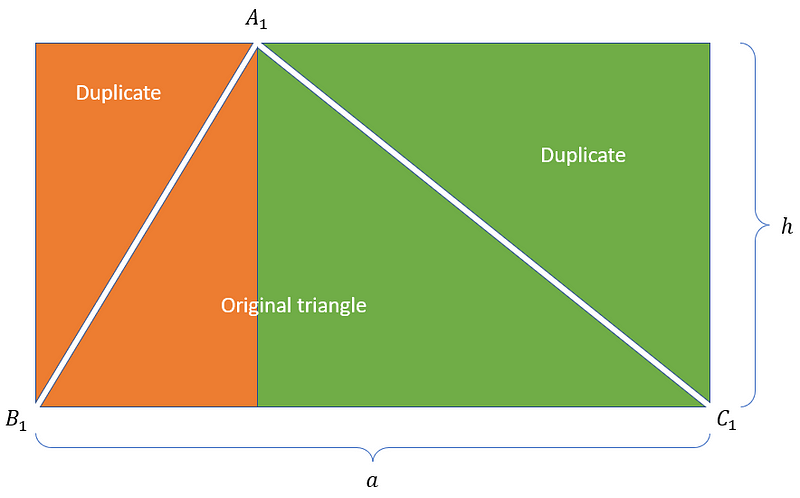
Now, envision a triangle ABC with a base 'a' and a height 'h'. By dropping a perpendicular from point A to the base, the triangle can be split into two right triangles. If you duplicate one of these right triangles and flip it across the hypotenuse, what do you create? A rectangle with dimensions 'a' and 'h'. As established earlier, the area of this rectangle is a × h. Since the rectangle comprises a triangle that was duplicated and rearranged, its area will be exactly double that of the original triangle. Therefore, the area of triangle ABC is given by the formula:
text{Area} = frac{1}{2} (a times h)
Exploring More Complex Scenarios
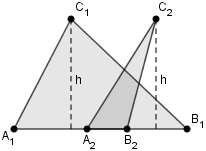
Now, let’s introduce another triangle, DEF, which shares the same height 'h' as triangle ABC. For clarity, we denote the bases of each triangle as AB and DE, respectively, both aligned along the same line, as illustrated below.
Taking the ratio of the areas of these two triangles leads us to the following conclusion:
frac{Area_{ABC}}{Area_{DEF}} = frac{Base_{AB}}{Base_{DE}}
In essence, we establish Theorem 1.6:
If two triangles share the same height, then the ratio of their areas corresponds to the ratio of their bases.
Introducing the Sine Function
Now, consider triangle ABC again, with point D positioned on line BC such that AD is perpendicular to BC. The area of triangle ABC can be defined as follows, utilizing the sine function:
Area_{ABC} = frac{1}{2} cdot BC cdot AD = frac{1}{2} cdot BC cdot AB cdot sin(angle ABC)
This representation allows us to express the area without directly using the height 'h'.
Theorem 1.7 states:
The area of triangle ABC can be expressed as:
Area_{ABC} = frac{1}{2} cdot AB cdot AC cdot sin(angle ABC)
This formulation proves beneficial when the height is not readily available. Alternatively, one can compute the height using the sine function and then apply the original area formula. Both methods yield identical results.
Visual Representations
The first video titled "How to Find the Area of a Triangle" provides a comprehensive overview of various methods to calculate triangle area, perfect for reinforcing the concepts discussed above.
The second video, "Area of a Triangle, Given 3 Sides, Heron's Formula," delves into Heron's formula for determining the area of a triangle when only the side lengths are known, expanding your understanding of triangle area calculations.
Conclusion
By exploring different methods for calculating the area of triangles—whether through geometric decomposition or the sine function—we broaden our mathematical toolkit. Each approach serves its purpose, depending on the information available and the context of the problem.